Linear Regression
机器学习线性回归复现
预测函数
$$
y_\theta(x)=\theta_0x+\theta_1b
$$
n元线性回归
$$
h_\theta(x)=\theta_0+\theta_1x1+\theta_2x2
$$
$$
h_\theta(x)=\sum^n_{i=0}{\theta_ix_i}= \theta^Tx
$$
损失函数 cost function
$$
J(\theta_0,\theta_1,….,\theta_n) = {1\over{2m}}\sum^{m}_{i=1}(h\theta(x^i)-y^i)^2
$$
梯度下降法
$$
\theta_j := \theta_j-\alpha{\partial\over\partial\theta_j}(\theta_0,\theta_i)
$$
Python实现
安装相关库
1 | import numpy as np |
准备数据
1 | data = np.array([[32, 31], [53, 68], [61, 62], [47, 71], [59, 87], [55, 78], [52, 79], [39, 59], [48, 75], [52, 71], |
读取数据
1 | x = data[:,0] |
定义损失函数
1 | def cost (w,b,data): |
对数据进行reshape
1 | x_new = x.reshape(-1,1) |
使用模型获取w,b参数
1 | lr = LinearRegression() |
调用损失函数
1 | cost = cost(w, b, data) |
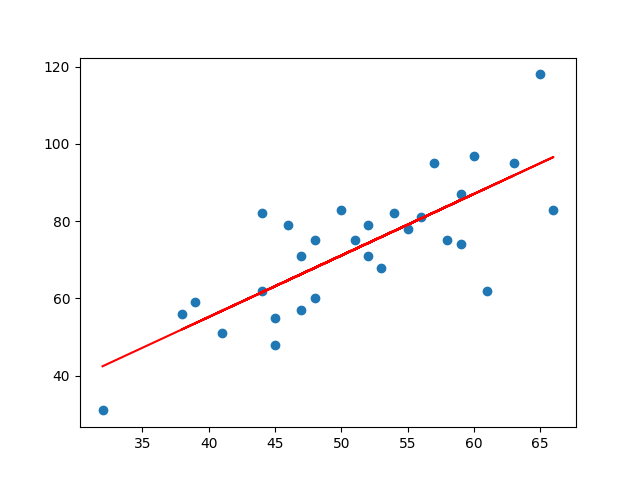
绘制图形
1 | plt.scatter(x,y) |
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 ZG's Web!
评论
